PointNet++
# Set Abstraction (SA) Layer
# Sampling Layer
Lets call the sampling layer $SL$.
- Input: $N\times 3$
- N points with $x,y,z$
- Output: $M\times 3$
- $M$ points with $x,y,z$ where points in $M$ are subset of $N$
- Method: Iterative Farthest Point Sampling (FPS)
- Start by choosing 1 random point
- Calculate distance for all remaining points to selected points.
- so each point will have an array keeping track of the distances
- take the minimum of the arrray, i.e. for each remaining point, set its distance to the closest selected point.
- Finally, select the point with the greatest distance
- Repeat step 2 $M-1$ more times
- 1D Example: Consider an array of points $P=[1,6,7,8,20]$,
- suppose the list of selected points $S=[7,20]$ , $P$ is now $[1,6,8]$
- we calculate distances: $$\begin{align*}dist_1=[6,19]\\ dist_6=[1,14]\\ dist_8=[1,12]\\ \end{align*}$$
- perform $min (dist_i)$$$\begin{align*}dist_1=6\\ dist_6=1\\ dist_8=1\\ \end{align*}$$
- now select the point with highest distance. i.e. $$\underset{i}{\operatorname{argmax}}(dist_i)=1$$
- So the next chosen point is 1. $S=[1,7,20]$ and $P=[6,8]$
# Grouping Layer
- Sampling Layer $SL$ yields $N’\times 3$ points.
- $N’$ centroids and $3:= x,y,z$ coordinates
- $SL:(N\times 3) \to (N’\times 3)$
- Input:
- $(N\times 3+ C)$: points before sampling and their feature vectors of len $C$
- $(N’\times d)$: predicted centroids
- Output:
- $(N’\times K \times (3+C))$: centroid + $K$ points within radius of $r$ along their features
- Method:
- Ball query - what if points within radius is $<K$? - what if no points (only centroid point)? - with if more than $K$ points?
# Multi-scale grouping (MSG)
- Due to nonuniformity of point clouds, we needs some more tricks to make feature learning more robust.
- One simple way is to applying grouping + pointnet multiple times then concat their features
- Dilated Group: implementation setting where you set a min radius.
- eg: $r=[0.2,0.4,0.8]$, then
- for $r=0.2$, sample within radius $[0,0.2]$
- for $r=0.4$, sample within radius $[0.2,0.4]$
- for $r=0.8$, sample within radius $[0.4,0.8]$
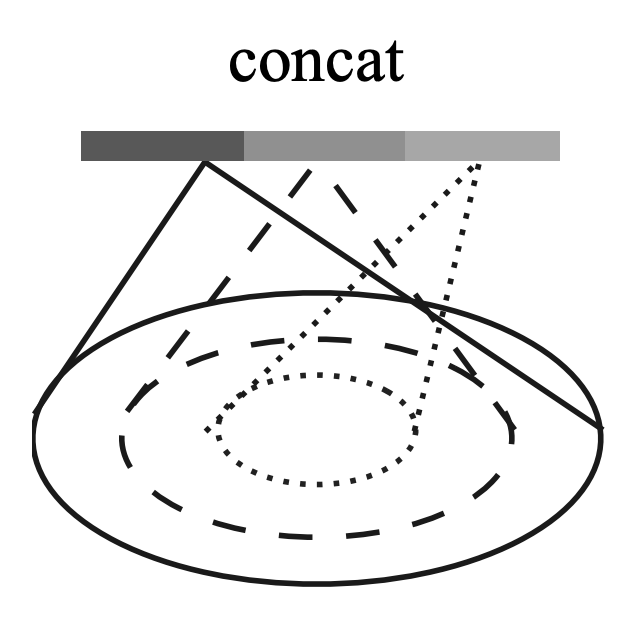
# Multi-resolution grouping (MRG)
- MSG works, but its computationally expensive, so this is an alternative method
- Consider a layer for input of points, we first apply set abstraction layer (sampling + grouping + pointnet), to yield a vector of features $L_1$. We then apply pointnet of the raw pointcloud (before set abstraction) to yield feature vector $L_2$. Then we concat the results $(L_1,L_2)$
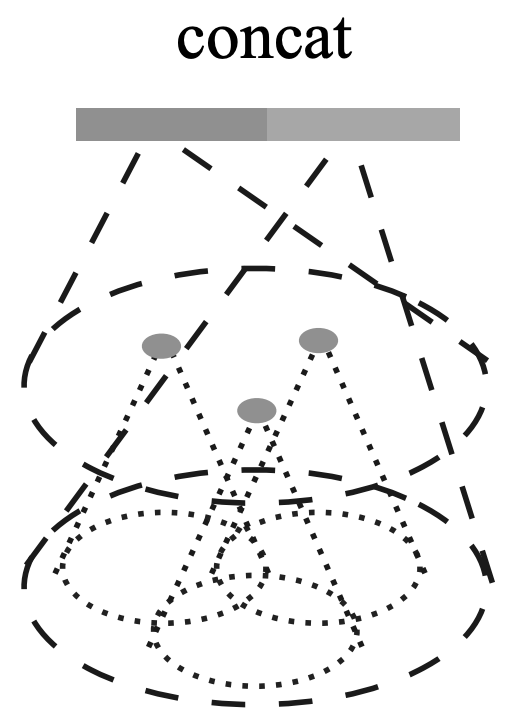
# PointNet Layer
essentially just a FC layer on each “ball” of points
- Input $(N’\times K \times (3+C))$.
- $N’$ local regions (balls of points)
- $K$ is num of balls in the ball
- $3+C = x,y,z+C \text{ features}$
- Output: $(N’\times (3+C’))$
- Method:
- for each point $x_j$ in a ball, transform it into a local coordinate frame relative to its centroid $\hat{x}$ $$x^{new}_j = x_j-\hat{x}$$
- Then we apply series of FC layers